加法定理

加法定理は以下になります。

\[\sin(x + y) = \sin x \ \cos y + \cos x \ \sin y\]
\[\cos(x + y) = \cos x \ \cos y - \sin x \ \sin y\]

加法定理からベクトルの回転の公式が得られます。

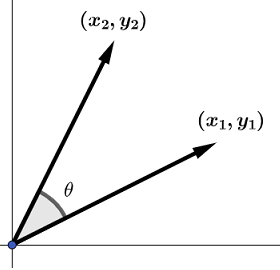
_images/rot-vec1.png
\[\begin{split}x_2 = x_1 \ \cos \theta - y_1 \ \sin \theta \\ y_2 = x_1 \ \sin \theta + y_1 \ \cos \theta\end{split}\]

順運動学

軸の角度から手先の位置と姿勢(角度)を求めることを順運動学と言います。

順運動学はベクトルの回転の公式を使って計算できます。

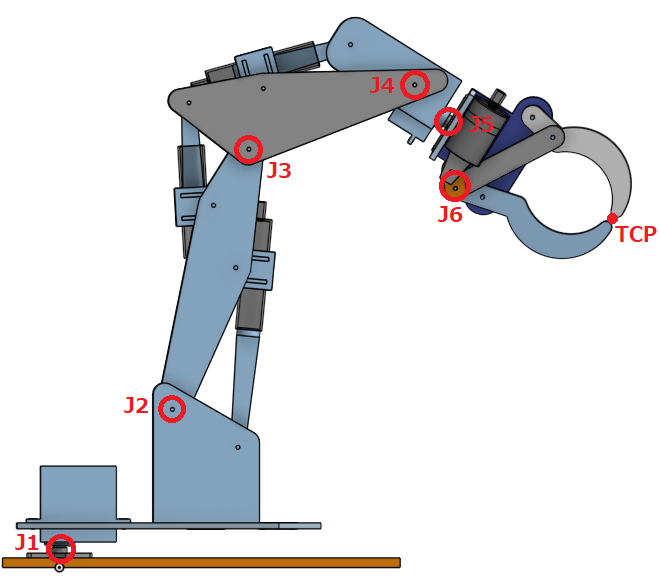
_images/front.png

このロボットアームには6個の可動軸があり、アームの根本からJ1, J2, J3, J4, J5, J6と言います。

アームの手先の位置をTCP(Tool Center Point)と言います。

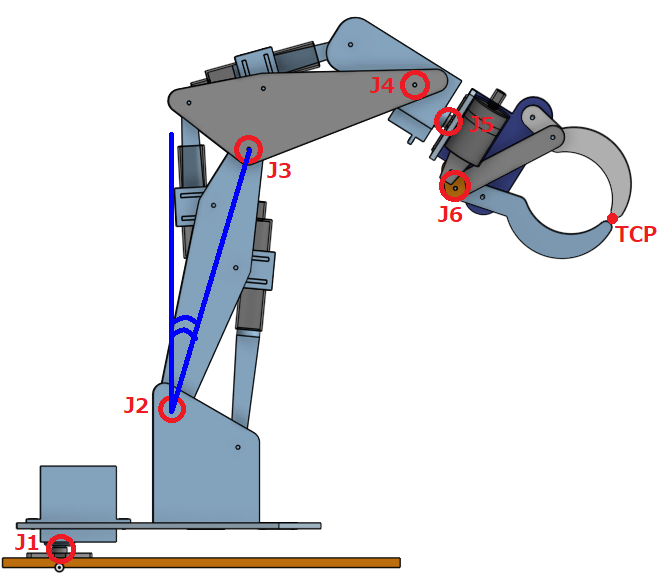
_images/rot-vec2.png

アームを真横から見るとJ1とJ2の位置は固定です。

J3の位置はJ2の回転角から求まります。

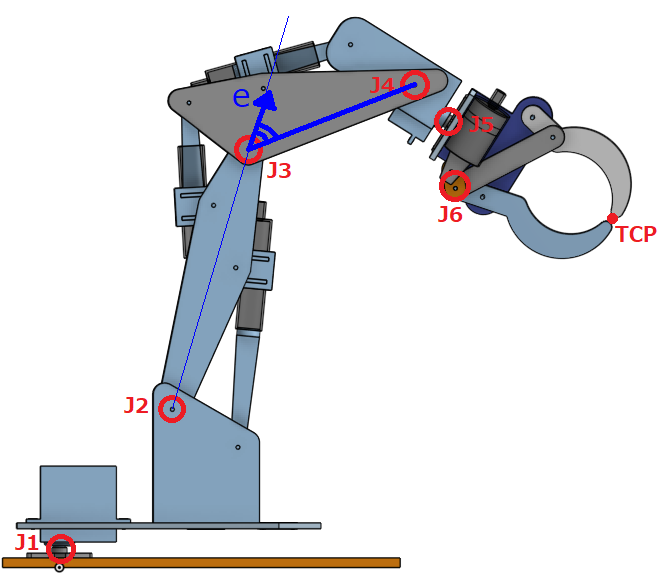
_images/rot-vec3.png
J2からJ3に向かう単位ベクトルをeとします。
J4の位置はベクトルの回転の公式を使い、eとJ3の回転角から求まります。

J5の位置も同様にベクトルの回転の公式を使い、J4の回転角から求まります。

J6はハンドを開閉させるだけなので位置は関係ありません。

TCPの位置もベクトルの回転の公式を使い、J4の回転角から求まります。

以上のように、加法定理を使って順運動学が解けます。