2曲線が接する条件
2曲線が接する条件は、歯車がかみ合う動きの説明に使います。
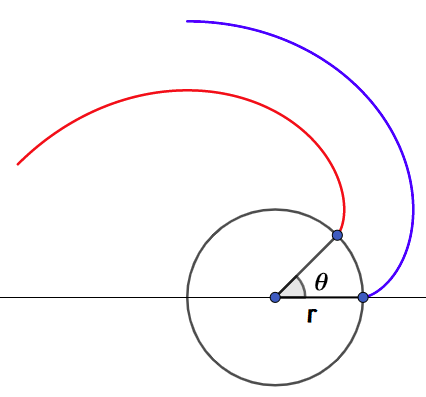
一般的な歯車の歯はインボリュート曲線の形をしています。
半径rの円に対するインボリュート曲線は以下の式になり、図で青色の曲線です。
\[\begin{split}\begin{equation}
\begin{split}
x = r \ (\cos t + t \sin t)
\\
y = r \ (\sin t - t \cos t)
\end{split}
\tag{1}
\end{equation}\end{split}\]
青色の曲線はX軸から開始していますが、X軸からθ回転した点から開始する場合は以下の式になり、赤色の曲線です。
\[\begin{split}\begin{equation}
\begin{split}
x = r \ (\cos (\theta + t) + t \sin (\theta + t))
\\
y = r \ (\sin (\theta + t) - t \cos (\theta + t))
\end{split}
\tag{2}
\end{equation}\end{split}\]
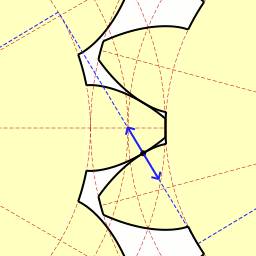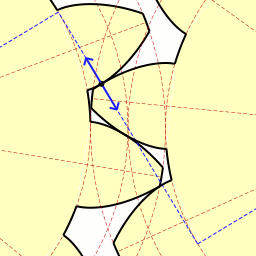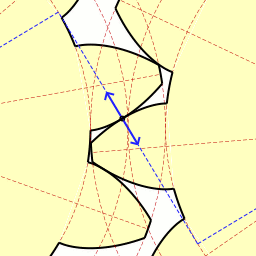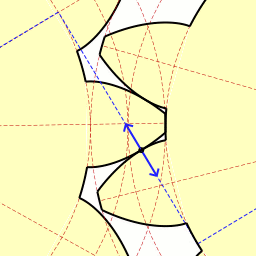
この図は2つの歯車がかみ合う動きを示しています。
歯車の接点が青色の線の上を移動しています。
青色の線を作用線と言います。
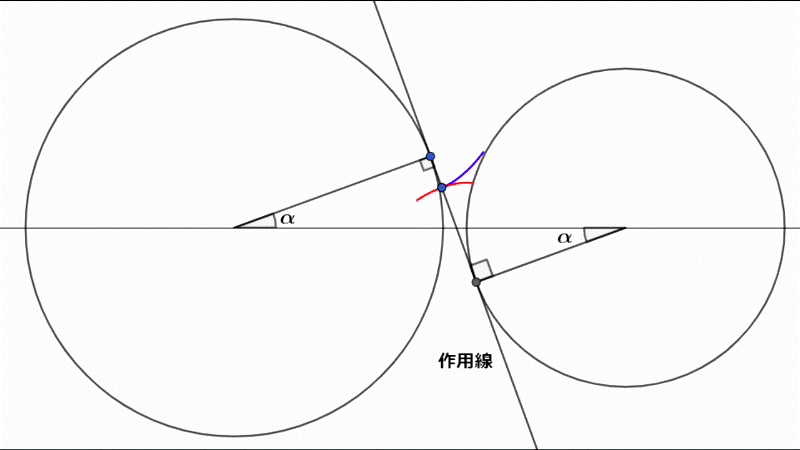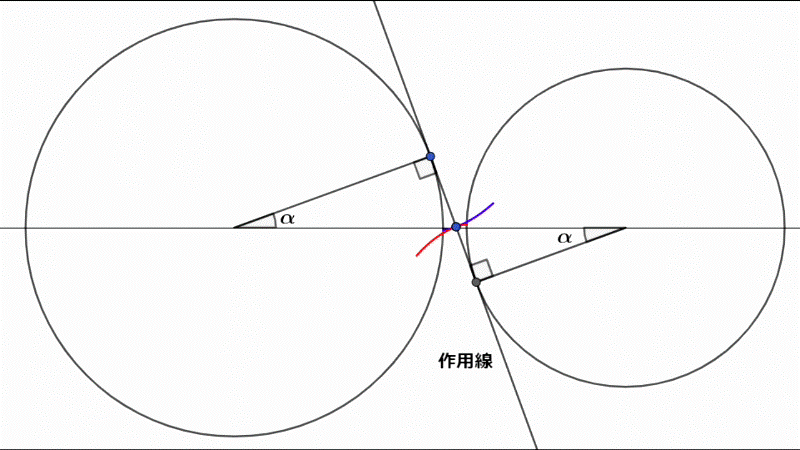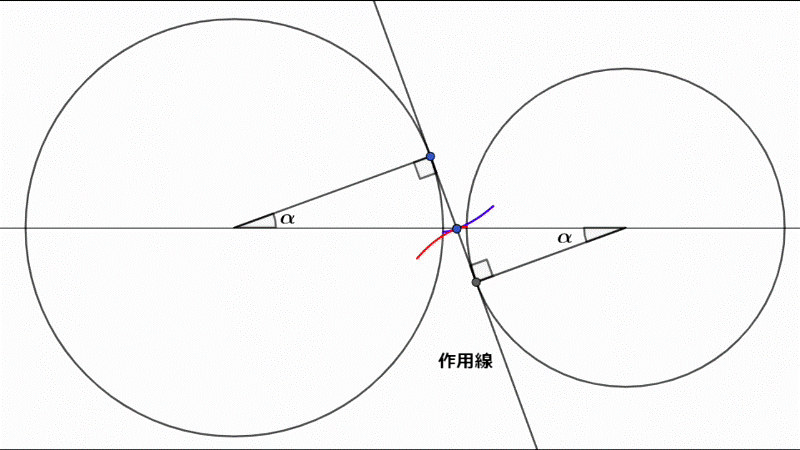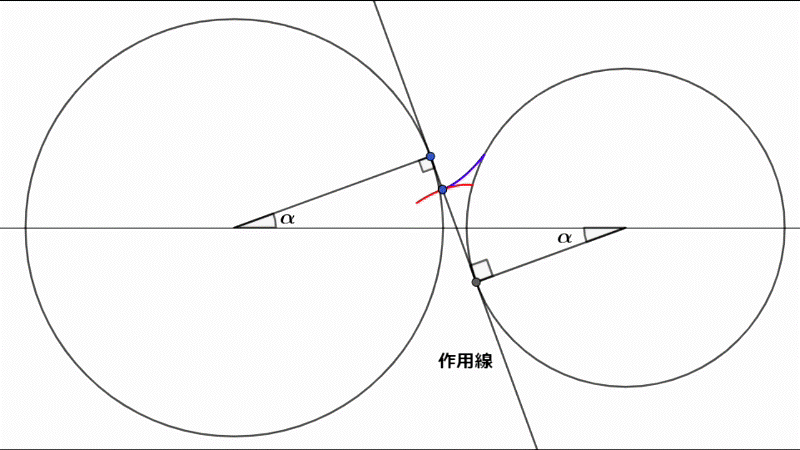
これは一対のインボリュート曲線に注目した図です。
2つの円に接する接線が作用線です。
接点の角度αを圧力角と言い、20°がよく使われます。
以下で2つの歯車が作用線でかみ合うことを証明します。
2曲線が接する条件は接点での接線の向きが同じであることです。
式(2)をtで微分します。
\[\begin{split}\begin{equation}
\begin{split}
\frac{dx}{dt} & = & r \ (- \sin (\theta + t) + \sin (\theta + t) + t \cos(\theta + t)) = r \ t \cos (\theta + t)
\\
\frac{dy}{dt} & = & r \ ( \cos (\theta + t) - \cos (\theta + t) + t \sin(\theta + t)) = r \ t \sin (\theta + t)
\end{split}
\tag{3}
\end{equation}\end{split}\]
一方式(2)の意味を考えると、作用線上にあるインボリュート曲線の点では \(\theta + t = \alpha\) です。
これを式(3)に代入すると接線のベクトルは以下になります。
\[(\frac{dx}{dt}, \frac{dy}{dt}) = r \ t (\cos(\alpha), \sin(\alpha))\]
作用線上ではインボリュート曲線の接線は常に \((\cos(\alpha), \sin(\alpha))\) と同じ向きなので、
2つのインボリュート曲線は作用線上で接します。
以上で2つの歯車が作用線でかみ合うことが証明できました。