ピタゴラスの定理と三角関数

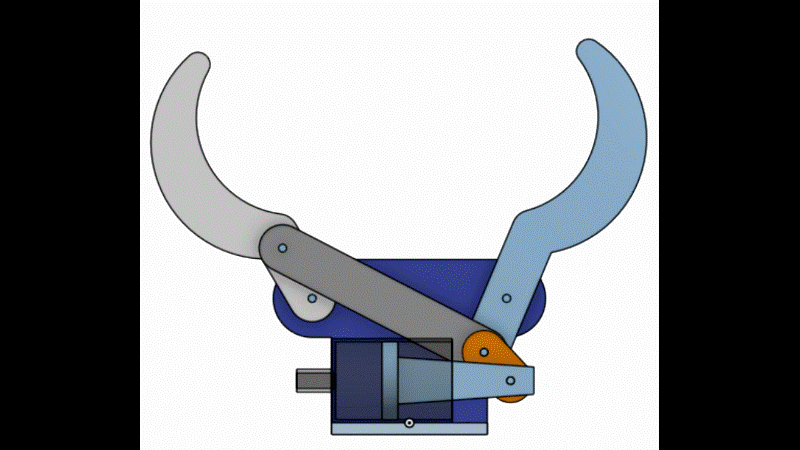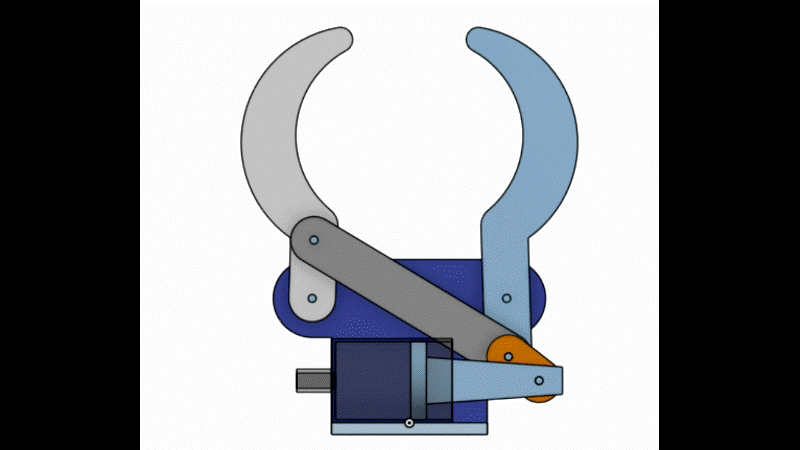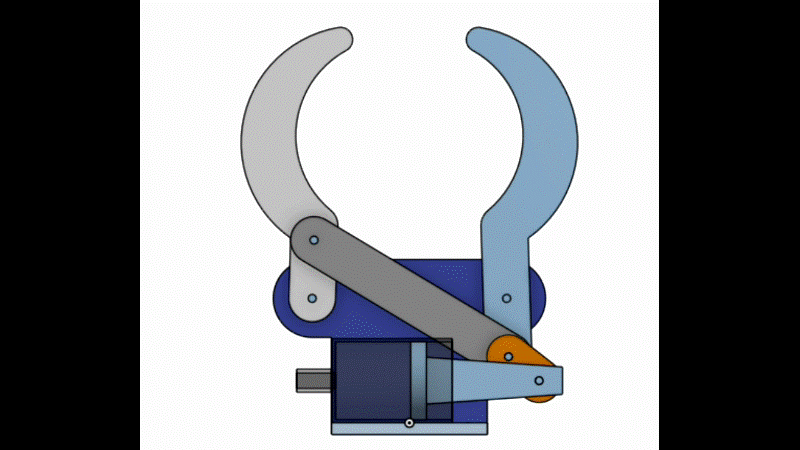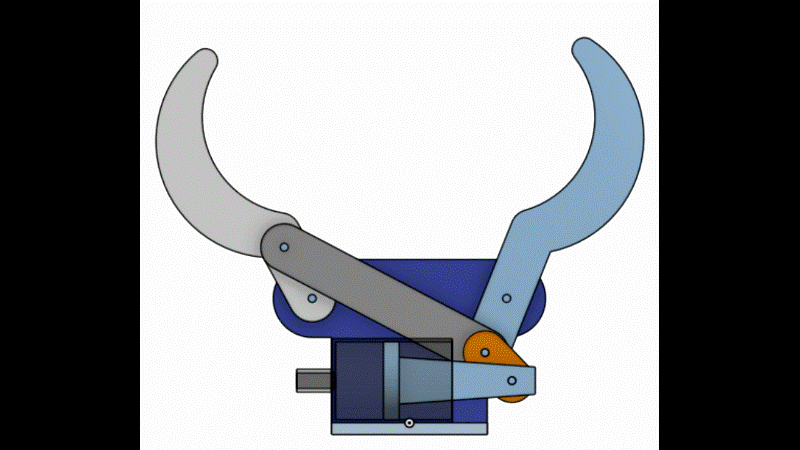
図のような機構をグリッパと言います。

グリッパの構造を調べるのに、ピタゴラスの定理と三角関数を使います。

右指と左指をつないでいる斜めの灰色の棒(リンク)があるので、注射器のピストンが動くと右指と左指が両方動きます。

右指の回転する角度と左指の回転する角度が同じように見えますが、実際は少しずれています。

以下でずれる理由を説明します。

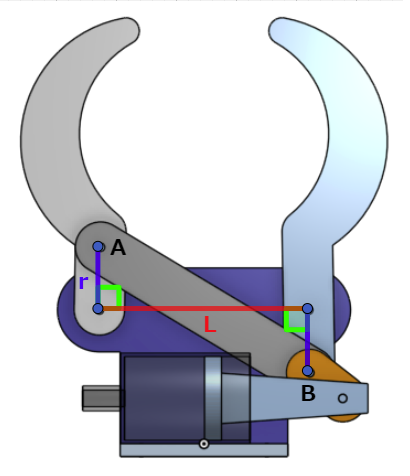
右指と左指の回転軸の距離(赤線)を L とします。

指の回転軸とリンクの回転軸との距離(青線)を r とします。

赤線と青線のなす角は \(\frac{\pi}{2}\) とします。

リンクの回転軸A, Bの距離はピタゴラスの定理から以下になります。

\[\overline{ AB } = \sqrt{ L^2 + (2 \ r)^2 }\]

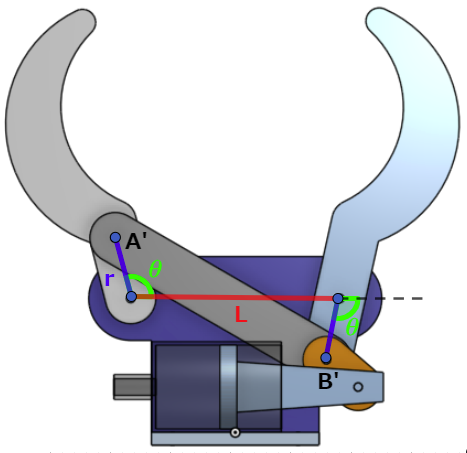
次に赤線と青線のなす角が \(\theta\) で、指の回転軸から r の距離にある点を A'とB' します。

A'とB' の距離は以下になります。

\[\overline{ A'B' } = \sqrt{ L^2 + (2 \ r \ \sin \theta)^2 }\]

\(AB\) と \(A'B'\) は一致しないので、右指と左指の回転角は同じでないことが分かります。

しかし、 \(\theta \fallingdotseq \frac{\pi}{2}\) なら \(\sin \theta \fallingdotseq 1\) なので、 \(\theta\) が \(\frac{\pi}{2}\) と大きく離れないようにグリッパを設計すれば、実用上は問題なさそうです。