三角関数の微分と積分

Ｓ字加減速​

モーターを滑らかに加速と減速をすることをＳ字加減速​と言います。​

急に加減速をすると、大きな電流が流れて過電流になる危険があるので
滑らかな加減速は重要です。

Ｓ字加減速​には一般に三角関数を使います。

まず、距離や速度の関係をまとめます。

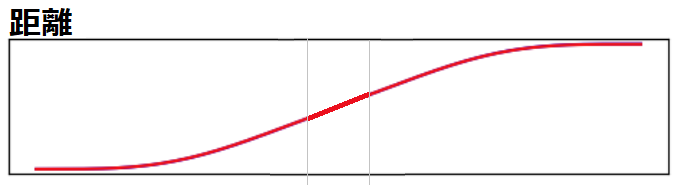
_images/dist.png

距離の微分が速度です。​

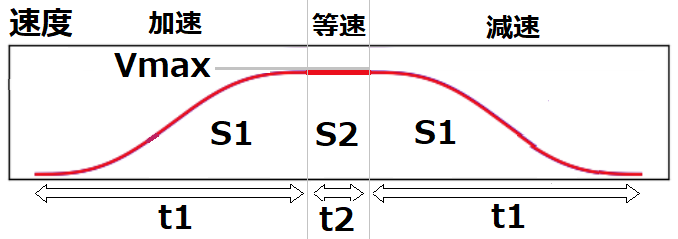
_images/vel.png
加減速時間を \(t_1\) 、等速時間を \(t_2\) とします。
加速中の移動距離を \(S_1\) 、等速での移動距離を \(S_2\) とします。
最高時速を \(v_{max}\) とします。
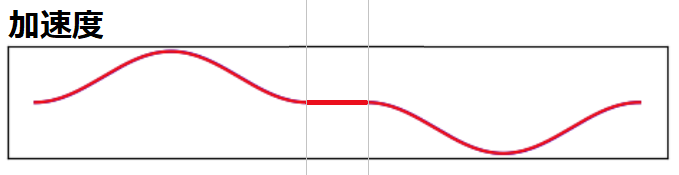
_images/acc.png

速度の微分が加速度です。​

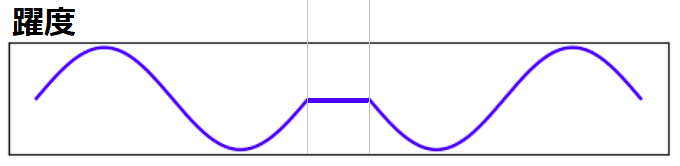
_images/jerk.png

加速度の微分を躍度と言います。​

躍度 \(\mathrm{jerk}\) を以下の式で定義します。

\[\begin{split}\begin{eqnarray} \mathrm{jerk}(t) = \begin{cases} A \ \sin(\omega t) & ( \boldsymbol{加速中} ) \\ 0 & ( \boldsymbol{等速中} ) \\ - A \ \sin(\omega t) & ( \boldsymbol{減速中} ) \end{cases} \end{eqnarray}\end{split}\]

以下では証明は省略して結果だけを書きます。

加速度 \(\mathrm{acc}\)

\[\mathrm{acc}(t) = \frac{A}{\omega} \ (1 - \cos(\omega t))\]

速度 \(\mathrm{vel}\)

\[\mathrm{vel}(t) = \frac{A}{\omega} \ (t - \frac{\sin(\omega t)}{\omega})\]

距離 \(S\)

\[S(t) = \frac{A}{\omega}( \frac{1}{2} t^2 + \frac{\cos(\omega t) - 1}{\omega^2} )\]

躍度の定義式の中のω

\[\omega = \frac{2 \pi}{t_1}\]

躍度の定義式の中のA

\[A = \frac{v_{max} \ \omega^2}{2 \ \pi}\]

加速中の移動距離 \(S_1\)

\[S_1 = \frac{v_{max} \ t_{1} }{2}\]

上の \(S_1\) の式はとても重要です。

実際にロボットアームを制御するときは、最高速度 \(v_{max}\) と加速時間 \(t_{1}\) を調節して、指定した距離を移動します。