モーター

最初にモーターに関連する物理量をまとめておきます。

力Fを加えて距離Lを移動したとき、仕事Wは以下で定義されます。

\[W = F \ L\]

仕事率Pは時間当たりの仕事です。

\[P = \frac{W}{t}\]

回転運動の場合、トルクTを加えて角度θだけ回転させたとき、仕事Wは以下で定義されます。

\[W = T \ \theta\]

回転運動の仕事率 \(P_m\) は時間当たりの仕事で、角速度を \(\omega\) とすると以下の式になります。

\[P_m = \frac{W}{t} = \frac{T \ \theta}{t} = T \ \omega\]

電力 \(P_e\) は、電圧Vと電流Iの積です。

\[P_e = V \ I\]

電力をモーターで動力に変換する場合 \(P_m = P_e\) なので以下の式になります。

\[T \ \omega = V \ I\]

実際は電力の変換の際に損失が発生するので、 \(\mu\) を変換効率とすると以下の式になります。

\[T \ \omega = V \ I \ \mu\]

フレミング左手の法則により、モータのトルクTは電流に比例します。 \(K_t\) はトルク定数です。

\[T = K_t \ I\]

以上を踏まえた上で、実際のモーターの仕様からモーターの特性のグラフを描いてみます。

上はプラモデルなどでよく使われるマブチモーターのFA-130RAの仕様です。

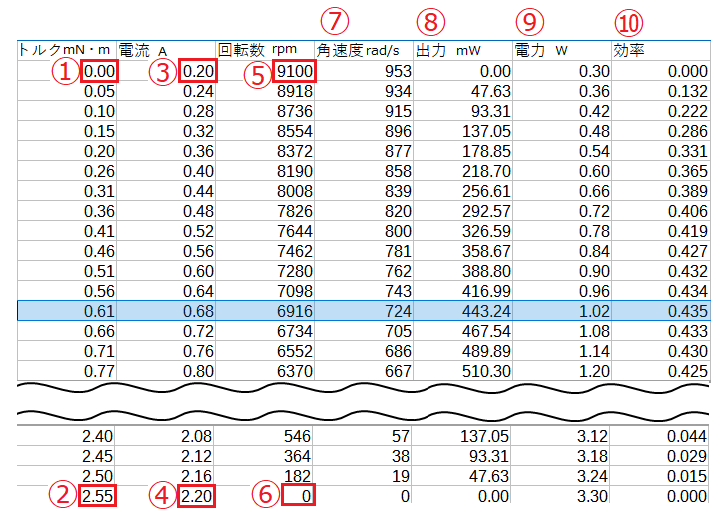
以下の手順で表計算ソフトに値を入れます。

最初の行には無負荷(NO LOAD)での値を入れ、最後の行には停止時(STALL)の値を入れます。

① トルクの最初の行に 0 を入れます。

② トルクの最後の行にSTALL TORQUEの 2.55 を入れます。

途中の行には比例計算した値を入れます。

③ 電流の最初の行にNO LOAD CURRENTの 0.20 を入れます。

④ 電流の最後の行にSTALL CURRENTの 2.20 を入れます。

途中の行には比例計算した値を入れます。

⑤ 回転数の最初の行にNO LOAD SPEEDの 9100 を入れます。

⑥ 回転数の最後の行に 0 を入れます。

途中の行には比例計算した値を入れます。

⑦ 角速度の列に 回転数 × 2 × π ÷ 60 の値を入れます。

⑧ 出力の列に トルク × 角速度 の値を入れます。

⑨ 電圧を1.5Vとして、電力の列に 1.5 × 電流 の値を入れます。

⑩ 効率の列に 0.001 × 出力 ÷ 電力 の値を入れます。

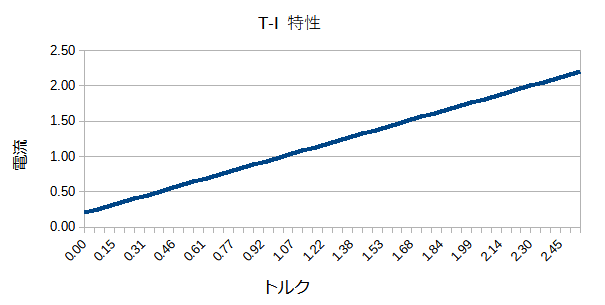
これはトルクと電流のグラフで、T-I特性と言います。

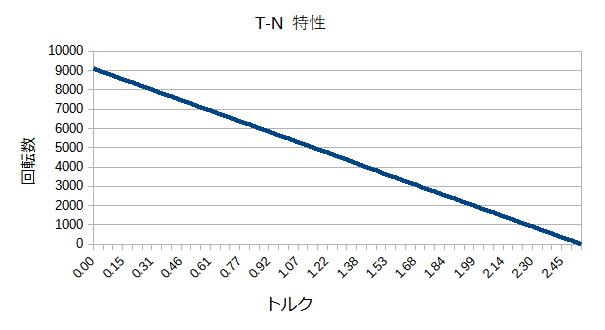
これはトルクと回転数のグラフで、T-N特性と言います。

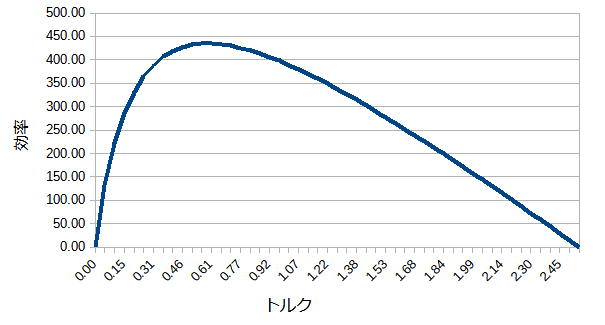
これはトルクと効率のグラフです。

モーターの仕様の最高効率(AT MAXIMUM EFFICIENCY)の欄は以下の値になっています。

速度(SPEED)	電流(CURRENT)	トルク(TORQUE)	出力(OUTPUT)
6990	0.66	0.59	0.43

これは表計算ソフトで最高効率の行(水色の行)とほぼ等しい値になっています。

微妙に値がずれるのは電力の変換効率 \(\mu\) が定数でないからかも知れません。